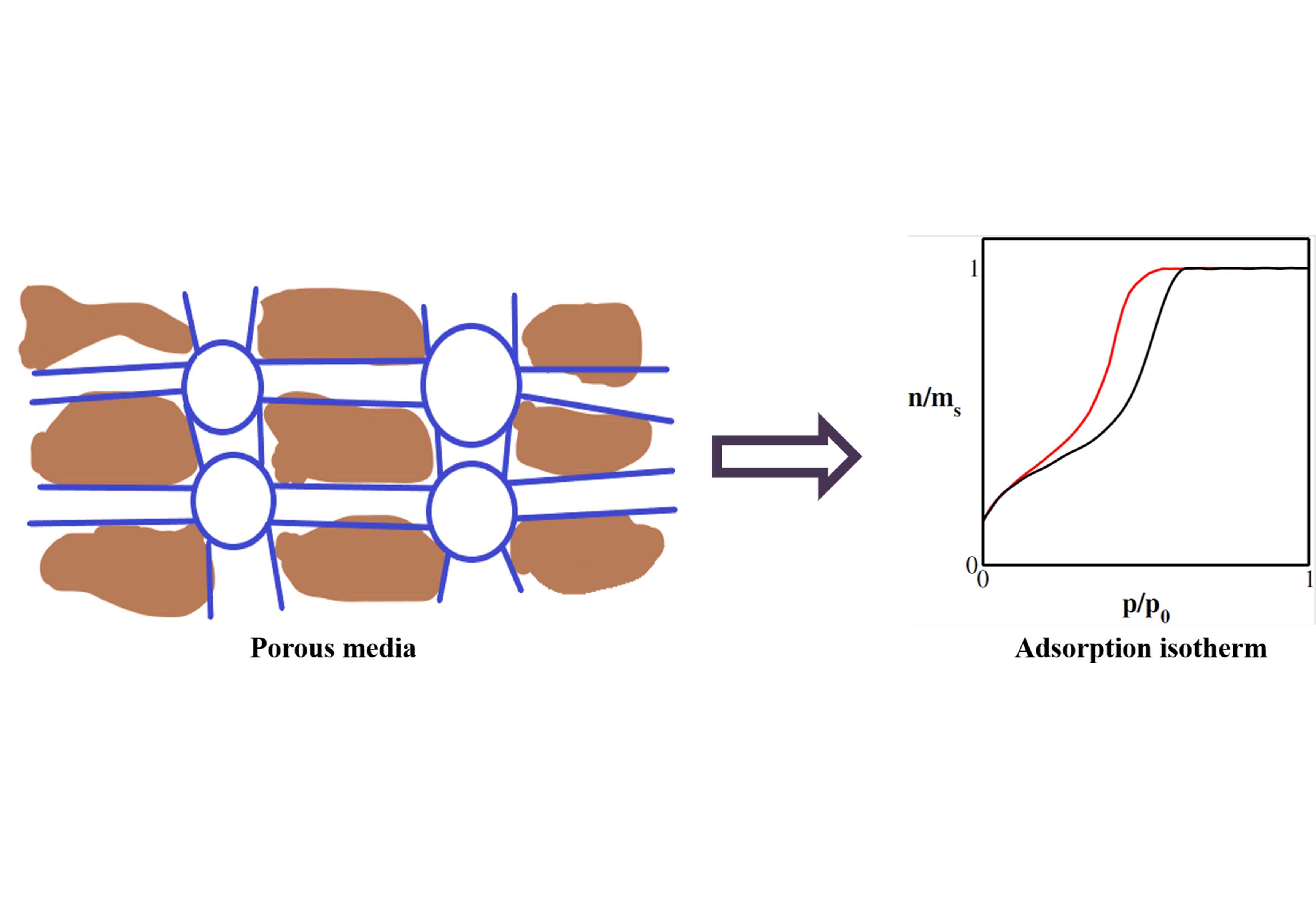
Review: Description of Porous Media and their Sorption Characteristics as Correlated Structures
DOI:
https://doi.org/10.29356/jmcs.v68i4.2269Keywords:
Adsorption isotherms, Physicochemical of Surfaces Academic Area, Porous mediaAbstract
This review presents an in-depth analysis of the progress and achievements in the study of porous structures by the Physicochemical of Surfaces Academic Area at the Universidad Autónoma Metropolitana, Iztapalapa's Chemistry Department. A straightforward model for depicting disordered structures has been introduced here, facilitating the discovery of correlations between adjacent elements within these structures. Such correlations have proven to be crucial in the classification and analysis of different disordered porous materials and have been instrumental in the interpretation and categorization of nitrogen adsorption isotherms.
Resumen. Este artículo proporciona una revisión completa de los avances y aportes realizados en la caracterización de estructuras porosas dentro del Área Académica de Fisicoquímica de Superficies del Departamento de Química de la Universidad Autónoma Metropolitana, Iztapalapa. Dentro de esta Área Académica se ha desarrollado un modelo simple para describir estructuras desordenadas, que permitió visualizar la correlación entre elementos vecinos que constituyen dichas estructuras. Estas correlaciones han resultado en un factor clave para clasificar y categorizar diversos medios porosos desordenados, además de servir como herramientas útiles para interpretar y clasificar las isotermas de adsorción del nitrógeno.
Downloads
References
Tovbin, Yu. K. The Molecular Theory of Adsorption in Porous Solids, 1st ed.; CRC Press, 2017. DOI: https://doi.org/10.1201/9781315116297.
Ghanbari, T.; Abnisa, F.; Wan Daud, W. M. A. A Review on Production of Metal Organic Frameworks (MOF) for CO2 Adsorption. Science of The Total Environment 2020, 707, 135090. DOI: https://doi.org/10.1016/j.scitotenv.2019.135090.
Verma, P.; Kuwahara, Y.; Mori, K.; Raja, R.; Yamashita, H. Functionalized Mesoporous SBA-15 Silica: Recent Trends and Catalytic Applications. Nanoscale 2020, 12, 11333–11363. DOI: https://doi.org/10.1039/D0NR00732C.
Characterization of Porous Solids and Powders: Surface Area, Pore Size and Density, [4. ed.], 1. repr. with some corr.; Lowell, S., Ed.; Particle technology series; Springer: Dordrecht, 2010.
Brunauer, S.; Emmett, P. H.; Teller, E. Adsorption of Gases in Multimolecular Layers. J. Am. Chem. Soc. 1938, 60, 309–319. DOI: https://doi.org/10.1021/ja01269a023.
Naderi, M. Chapter Fourteen - Surface Area: Brunauer–Emmett–Teller (BET). In Progress in Filtration and Separation; Tarleton, S., Ed.; Academic Press: Oxford, 2015; pp 585–608. DOI: https://doi.org/10.1016/B978-0-12-384746-1.00014-8.
Wu, J.; Li, Z. Density-Functional Theory for Complex Fluids. Annu. Rev. Phys. Chem. 2007, 58, 85–112. DOI: https://doi.org/10.1146/annurev.physchem.58.032806.104650.
Wu, J. Density Functional Theory for Chemical Engineering: From Capillarity to Soft Materials. AIChE Journal 2006, 52, 1169–1193. DOI: https://doi.org/10.1002/aic.10713.
Makkar, P.; Ghosh, N. N. A Review on the Use of DFT for the Prediction of the Properties of Nanomaterials. RSC Adv. 2021, 11, 27897– 27924. DOI: https://doi.org/10.1039/D1RA04876G.
Gubbins, K. E.; Sliwinska-Bartkowiak, M.; Suh, S.-H. Molecular Simulations of Phase Transitions in Pores. Molecular Simulation 1996, 17, 333– 367. DOI: https://doi.org/10.1080/08927029608024116.
Segura, C. J.; Vakarin, E. V.; Chapman, W. G.; Holovko, M. F. A Comparison of Density Functional and Integral Equation Theories vs Monte Carlo Simulations for Hard Sphere Associating Fluids near a Hard Wall. The Journal of Chemical Physics 1998, 108, 4837–4848. DOI: https://doi.org/10.1063/1.475893.
Zaragoza, A.; Gonzalez, M. A.; Joly, L.; López Montero, I.; Canales, M. A.; Benavides, A. L.; Valeriani, C. Molecular Dynamics Study of Nanoconfined TIP4P/2005 Water: How Confinement and Temperature Affect Diffusion and Viscosity. Phys. Chem. Chem. Phys. 2019, 21, 13653–13667. DOI: https://doi.org/10.1039/C9CP02485A.
Yuan, Z.; He, G.; Li, S. X.; Misra, R. P.; Strano, M. S.; Blankschtein, D. Gas Separations Using Nanoporous Atomically Thin Membranes: Recent Theoretical, Simulation, and Experimental Advances. Advanced Materials 2022, 34, 2201472. DOI: https://doi.org/10.1002/adma.202201472.
Yuan, Z.; Govind Rajan, A.; He, G.; Misra, R. P.; Strano, M. S.; Blankschtein, D. Predicting Gas Separation through Graphene Nanopore Ensembles with Realistic Pore Size Distributions. ACS Nano 2021, 15, 1727–1740. DOI: https://doi.org/10.1021/acsnano.0c09420.
Wang, Y.; Fan, Z.; Qian, P.; Ala-Nissila, T.; Caro, M. A. Structure and Pore Size Distribution in Nanoporous Carbon. Chem. Mater. 2022, 34, 617–628. DOI: https://doi.org/10.1021/acs.chemmater.1c03279.
Iftimie, R.; Minary, P.; Tuckerman, M. E. Ab Initio Molecular Dynamics: Concepts, Recent Developments, and Future Trends. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 6654–6659. DOI: https://doi.org/10.1073/pnas.0500193102.
Barrett, E. P.; Joyner, L. G.; Halenda, P. P. The Determination of Pore Volume and Area Distributions in Porous Substances. I. Computations from Nitrogen Isotherms. J. Am. Chem. Soc. 1951, 73, 373–380. DOI: https://doi.org/10.1021/ja01145a126.
Broekhoff, J. Studies on Pore Systems in Catalysts IX. Calculation of Pore Distributions from the Adsorption Branch of Nitrogen Sorption Isotherms in the Case of Open Cylindrical Pores A. Fundamental Equations. Journal of Catalysis 1967, 9, 8–14. DOI: https://doi.org/10.1016/0021-9517(67)90174-1.
Everett, D. H.; Haynes, J. M. Model Studies of Capillary Condensation. I. Cylindrical Pore Model with Zero Contact Angle. Journal of Colloid and Interface Science 1972, 38, 125–137. DOI: https://doi.org/10.1016/0021-9797(72)90228-7.
Feng, Q.; Xing, X.; Wang, S.; Liu, G.; Qin, Y.; Zhang, J. CO2 Diffusion in Shale Oil Based on Molecular Simulation and Pore Network Model. Fuel 2024, 359, 130332. DOI: https://doi.org/10.1016/j.fuel.2023.130332.
García-Salaberri, P. A.; Zenyuk, I. V. A General Purpose Tool for Modeling Multifunctional Thin Porous Media (POREnet): From Pore Network to Effective Property Tensors. Heliyon 2024, 10, e26253. DOI: https://doi.org/10.1016/j.heliyon.2024.e26253.
Söllner, J.; Neimark, A.; Thommes, M. Development and Application of an Advanced Percolation Model for Pore Network Characterization by Physical Adsorption. July 23, 2024. DOI: https://doi.org/10.26434/chemrxiv-2024-h9zlm-v3.
A Model of Adsorption-Desorption Hysteresis in Which Hysteresis Is Primarily Developed by the Interconnections in a Network of Pores. Proc. R. Soc. Lond. A 1983, 390, 47–72. DOI: https://doi.org/10.1098/rspa.1983.0122.
Determination of the Pore-Size Distributions and Pore-Space Interconnectivity of Vycor Porous Glass from Adsorption-Desorption Hysteresis Capillary Condensation Isotherms. Proc. R. Soc. Lond. A 1988, 415, 453–486. DOI: https://doi.org/10.1098/rspa.1988.0023.
Neimark, A. V. Percolation Theory of Capillary Hysteresis Phenomena and Its Application for Characterization of Porous Solids. In Studies in Surface Science and Catalysis; Elsevier, 1991; Vol. 62, pp 67–74. DOI: https://doi.org/10.1016/S0167-2991(08)61310-5.
Seaton, N. A. Determination of the Connectivity of Porous Solids from Nitrogen Sorption Measurements. Chemical Engineering Science 1991, 46, 1895–1909. DOI: https://doi.org/10.1016/0009-2509(91)80151-N.
Mayagoitia, V.; Javier Cruz, M.; Rojas, F. Mechanistic Studies of Capillary Processes in Porous Media. Part 1.—Probabilistic Description of Porous Media. J. Chem. Soc., Faraday Trans. 1 1989, 85, 2071. DOI: https://doi.org/10.1039/f19898502071.
Mayagoitia, V.; Rojas, F.; Kornhauser, I.; Pérez Aguilar, H. Modeling of Porous Media and Surface Structures: Their True Essence as Networks. Langmuir 1997, 13, 1327–1331. DOI: https://doi.org/10.1021/la950812m.
Riccardo, J. L.; Steele, W. A.; Cuesta, A. J. R.; Zgrablich, G. Pure Monte Carlo Simulation of Model Heterogeneous Substrates: From Random Surfaces to Many-Site Correlations. Langmuir 1997, 13, 1064–1072. DOI: https://doi.org/10.1021/la9510036.
Román-Alonso, G.; Rojas-González, F.; Aguilar Cornejo, M.; Cordero-Sánchez, S.; Castro-García, M. A. In-Silico Simulation of Porous Media: Conception and Development of a Greedy Algorithm. Microporous and Mesoporous Materials 2011, 137, 18–31. DOI: https://doi.org/10.1016/j.micromeso.2010.08.016.
Riccardo, J. L.; Pereyra, V.; Zgrablich, G.; Rojas, F.; Mayagoitia, V.; Kornhauser, I. Characterization of Energetic Surface Heterogeneity by a Dual Site-Bond Model. Langmuir 1993, 9, 2730–2736. DOI: https://doi.org/10.1021/la00034a037.
Metropolis, N.; Rosenbluth, A. W.; Rosenbluth, M. N.; Teller, A. H.; Teller, E. Equation of State Calculations by Fast Computing Machines. The Journal of Chemical Physics 1953, 21, 1087– 1092. https://doi.org/10.1063/1.1699114.
Bhanot, G. The Metropolis Algorithm. Rep. Prog. Phys. 1988, 51, 429–457. DOI: https://doi.org/10.1088/0034-4885/51/3/003.
Cordero Sánchez, S. Simulación de redes porosas por métodos de Monte Carlo. Maestría en Ciencias, Universidad Autónoma Metropolitana, 1998, p ht24wj79w. DOI: https://doi.org/10.24275/uami.ht24wj79w.
Sapag, K.; Bulnes, F.; Rizzotto, M.; Riccardo, J. L.; Zgrablich, G. On the Topology of Correlated Energies on Heterogeneous Surfaces. J. Phys.: Condens. Matter 1993, 5, A241–A242. https://doi.org/10.1088/0953-8984/5/33A/080.
Cruz, O.; Hidalgo, R.; Alas, S.; Cordero, S.; Meraz, L.; Lopez, R.; Dominguez, A. Is the Alexander–Orbach Conjecture Suitable for Treating Diffusion in Correlated Percolation Clusters? Adsorption Science & Technology 2011, 29, 663–676. DOI: https://doi.org/10.1260/0263-6174.29.7.663.
Tellez González, A. L. Estudio fractal de la reacción de oxidación de CO en Pt(100) por Monte Carlo. Maestría en Ciencias, Universidad Autónoma Metropolitana, Mexico City, 2022.
Cordero-Sánchez, S.; Rojas-González, F.; Román-Alonso, G.; Castro-García, M. A.; Aguilar Cornejo, M.; Matadamas-Hernández, J. Pore Networks Subjected to Variable Connectivity and Geometrical Restrictions: A Simulation Employing a Multicore System. Journal of Computational Science 2016, 16, 177–189. DOI: https://doi.org/10.1016/j.jocs.2016.06.003.
Paterson, L. Radial Fingering in a Hele Shaw Cell. J. Fluid Mech. 1981, 113, 513. https://doi.org/10.1017/S0022112081003613.
Mayagoitia, V.; Rojas, F.; Kornhauser, I.; Zgrablich, G.; Faccio, R. J.; Gilot, B.; Guiglion, C. Refinements of the Twofold Description of Porous Media. Langmuir 1996, 12, 211–216. DOI: https://doi.org/10.1021/la940704k.
Ramirez-Cuesta, A. J.; Cordero, S.; Rojas, F.; Faccio, R. J.; Riccardo, J. L. On Modeling, Simulation and Statistical Properties of Realistic Three Dimensional Porous Networks. Journal of Porous Materials 2001, 8, 61–76. DOI: https://doi.org/10.1023/A:1026526502692.
Cordero, S.; Rojas, F.; Riccardo, J. L. Simulation of Three-Dimensional Porous Networks. Colloids and Surfaces A: Physicochemical and Engineering Aspects 2001, 187–188, 425–438. https://doi.org/10.1016/S0927-7757(01)00610-0.
Gonzalez Mendez, A.; Roman Alonso, G.; Rojas Gonzalez, F.; Castro Garcia, M. A.; Aguilar Cornejo, M.; Cordero Sanchez, S. Construction of Porous Networks Subjected to Geometric Restrictions by Using OpenMP. In 2014 IEEE International Parallel & Distributed Processing Symposium Workshops; IEEE: Phoenix, AZ, 2014; pp 1189–1197. DOI: https://doi.org/10.1109/IPDPSW.2014.134.
Matadamas, J.; Roman, G.; Rojas, F.; Castro, M.; Cordero, S.; Aguilar, M. Pore Network Simulation via Monte Carlo Algorithms on GPUs. IEEE Latin Am. Trans. 2014, 12, 491–498. https://doi.org/10.1109/TLA.2014.6827878.
Matadamas-Hernández, J.; Román-Alonso, G.; Rojas-González, F.; Castro-García, M. A.; Boukerche, A.; Aguilar-Cornejo, M.; Cordero Sánchez, S. Parallel Simulation of Pore Networks Using Multicore CPUs. IEEE Trans. Comput. 2014, 63, 1513–1525. DOI: https://doi.org/10.1109/TC.2012.197.
Halsey, G. Physical Adsorption on Non-Uniform Surfaces. The Journal of Chemical Physics 1948, 16, 931–937. DOI: https://doi.org/10.1063/1.1746689.
Casanova, F.; Chiang, C. E.; Li, C.-P.; Schuller, I. K. Direct Observation of Cooperative Effects in Capillary Condensation: The Hysteretic Origin. Applied Physics Letters 2007, 91, 243103. https://doi.org/10.1063/1.2822815.
48. Sing, K. S. W. Reporting Physisorption Data for Gas/Solid Systems with Special Reference to the Determination of Surface Area and Porosity (Recommendations 1984). Pure and Applied Chemistry 1985, 57, 603–619. DOI: https://doi.org/10.1351/pac198557040603.
Gregg, S. J.; Sing, K. S. W.; Salzberg, H. W. Adsorption Surface Area and Porosity. J. Electrochem. Soc. 1967, 114, 279C. DOI: https://doi.org/10.1149/1.2426447.
Morishige, K. Hysteresis Critical Point of Nitrogen in Porous Glass: Occurrence of Sample Spanning Transition in Capillary Condensation. Langmuir 2009, 25, 6221–6226. DOI: https://doi.org/10.1021/la900022s.
Libby, B.; Monson, P. A. Adsorption/Desorption Hysteresis in Inkbottle Pores: A Density Functional Theory and Monte Carlo Simulation Study. Langmuir 2004, 20, 4289–4294. DOI: https://doi.org/10.1021/la036100a.
Ravikovitch, P. I.; Neimark, A. V. Density Functional Theory of Adsorption in Spherical Cavities and Pore Size Characterization of Templated Nanoporous Silicas with Cubic and Three-Dimensional Hexagonal Structures. Langmuir 2002, 18, 1550–1560. DOI: https://doi.org/10.1021/la0107594.
Rojas, F.; Kornhauser, I.; Felipe, C.; Esparza, J. M.; Cordero, S.; Domínguez, A.; Riccardo, J. L. Capillary Condensation in Heterogeneous Mesoporous Networks Consisting of Variable Connectivity and Pore-Size Correlation. Phys. Chem. Chem. Phys. 2002, 4, 2346–2355. https://doi.org/10.1039/b108785a.
Stauffer, D.; Aharony, A. Introduction To Percolation Theory, 0 ed.; Taylor & Francis, 2018. https://doi.org/10.1201/9781315274386.
55. Hidalgo-Olguín, D. R.; Cruz-Vázquez, R. O.; Alas-Guardado, S. J.; Domínguez-Ortiz, A. Lacunarity of Classical Site Percolation Spanning Clusters Built on Correlated Square Lattices. Transp Porous Med 2015, 107, 717–729. DOI: https://doi.org/10.1007/s11242-015-0463-3.
Everett, D. H. A General Approach to Hysteresis. Part 3.—A Formal Treatment of the Independent Domain Model of Hysteresis. Trans. Faraday Soc. 1954, 50, 1077–1096. DOI: https://doi.org/10.1039/tf9545001077.
Esparza, J. M.; Ojeda, M. L.; Campero, A.; Domı́nguez, A.; Kornhauser, I.; Rojas, F.; Vidales, A. M.; López, R. H.; Zgrablich, G. N2 Sorption Scanning Behavior of SBA-15 Porous Substrates.
Downloads
Published
Issue
Section
License
Copyright (c) 2024 Salomon Cordero Sanchez, Juan M. Esparza-Schulz, Ilich A. Ibarra, Víctor M. Trejos, Annabel L. Tellez-Gonzalez, Juan Villegas-Cortez, Graciela Roman-Alonso, Salomón J. Alas

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Authors who publish with this journal agree to the following terms:
- Authors retain copyright and grant the journal right of first publication with the work simultaneously licensed under a Creative Commons Attribution License that allows others to share the work with an acknowledgement of the work's authorship and initial publication in this journal.
- Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgement of its initial publication in this journal.